Home Examples How to solve Get iOS app FAQ

OK, so you know how to solve easy kaodokus. But how do you even get started on the hard ones? Well, here is an example that really shows off the particular complexities that can present themselves in kaodokus. It’s a puzzle with chaotic rather than square outlined areas, and four additional gray areas where every symbol has to occur once as well. Plenty of opportunities for interaction between all those different regions! And of course, not a single full symbol is given.

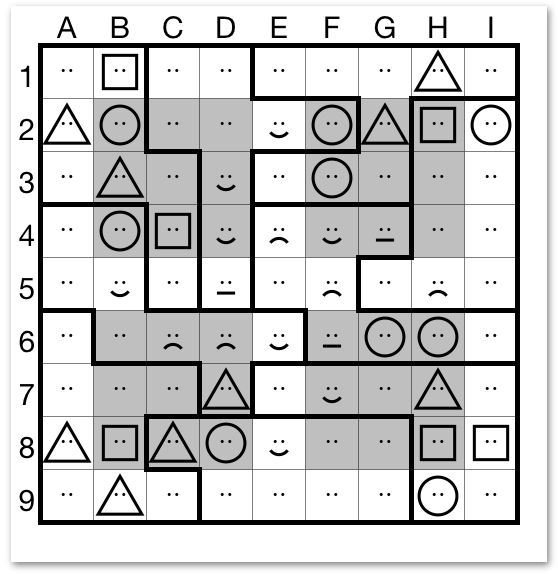
Here are some of the things you can find to get started (all independent from each other):

• Look at the puzzle piece at the top that contains the three happy mouths E2, D3 and D4. One of those three has to be the happy circle. Actually, make that either D3 or D4 since E2 cannot be a circle. But even without that latter insight, you would find that B2 is a neighbour of all three of these possible locations (same row as E2, and same gray area as D3/D4). And so is F2, obviously. That leaves I2 as the only possible location of the happy circle in the second row.
• The lower right gray area has to contain a happy square and a sad square somewhere. F8 and G8 are impossible because of the three squares in the same row. That leaves F7, G7 and H8 for those two symbols. All of these are in the lower right puzzle piece containing I8. Ergo, I8 is neither the happy nor the sad square, and must therefore be neutral.
• Let’s look at the puzzle piece near the middle, the one containing E5. Try to fit the happy square and the happy triangle in there. E5 cannot be happy since that column already has three mouths, so only F4 and I6 remain. We don’t know which is which, but we can certainly draw the happy mouth in I6 and make a mental note that this pair of cells has to contain the happy square and triangle. That also means the happy circle has to be in G6 or H6, which is useful information for column E…
• The triangle in D7, whatever its mouth may be, must have a twin with the same mouth somewhere in the bottom right puzzle piece. That twin cannot be in the same row (there can be other triangles there, and indeed there already is one in H7, but not the same one as D7) and therefore it must be in I9 since that’s the only free spot left for it. So we can add a triangle in I9, and make a mental note that it will have the same mouth as D7. If we find I9 later on, we can immediately add the same mouth in D7 and vice versa.
• The eighth row is missing two circles. F8 and G8 can be circles, but not both of them since that would make four circles in that gray area. That means there must be a circle in E8 as well. An alternative way of looking at this is by noticing that the circles in G6 and H6 must have twins (with the same pair of mouths) in the eighth row, but outside of the common gray area. That leaves only D8 and E8, so you can add the circle in E8.
• The happy mouth in F7 must have a twin in the puzzle piece above it, but not in any common area. Since E5 cannot be a fourth happy mouth in that column, F4 is in the same column as F7, and G6/H6 are in the same gray area, that only leaves I6. Of course we already found that mouth earlier, but this just shows you could have stumbled upon it in more than one way. And you now have extra information: if you happen to find the shape in I6, you can immediately apply the same shape in F7 or vice versa. You know that those symbols are one and the same even though you don’t have the full information yet.
• The square in I8 has to have a twin in the lower right gray area. The only cell in that area that doesn’t share a puzzle piece or a row with I8 and that can contain a square, is F6. That means I8 and F6 are both neutral squares.
• Now I’m going to show you a trick that might seem farfetched at first but which, once you get the hang of it, will turn out to be an incredibly versatile way of making easy progress in chaotic kaodokus. Look at the bottom three rows together. They must contain all symbols exactly three times, once in every row. Now look at the bottom three puzzle pieces. They too, must together contain all symbols exactly three times. Notice that these two conglomerate areas (the three rows vs. the three puzzle pieces) have almost all cells in common, except for D7 (in the rows, but not in the puzzle pieces) and A6 (in one of the three puzzle pieces but not in the bottom three rows). Now think about that for a minute. If you would know the contents of the 26 shared cells, you would also know the one symbol that was missing to make three sets of nine different symbols. And that symbol would have to be in D7, to complete the three rows, but also in A6 to complete the three puzzle pieces. In other words, A6 and D7 are one and the same, so you can put a triangle in A6.
• Now let’s apply the same trick in a more complicated way. Look at the three leftmost columns, and the three puzzle pieces bordering on the left edge of the puzzle. Using the line between columns C and D as a visual guide, you can see that D6/E6/D7 are “sticking out” of the left three columns, while C1/C2/C8 are part of other puzzle pieces. That means D6/E6/D7 must match C1/C2/C8 (both triplets contain the three missing symbols that must be added to the 24 shared cells to make three complete sets of 9). Now, C8 cannot match D7 nor D6 because they are in the same gray area. That only leaves C8 = E6, both are happy triangles.